Un alternateur présente un fonctionnement dit autonome lorsqu’il est le seul à fournir de l’énergie électrique à un réseau ou à un récepteur.
C’est par exemple le cas d’un alternateur alimentant l’installation électrique d’un chantier ou en secours une installation prioritaire (hôpital, central téléphonique, etc.).
Les applications de l’alternateur autonome est limitée mais en principe chaque alternateur peut être supposé autonome jusqu’à ce qu’il ne soit pas branché dans un réseau et la théorie est applicable dans tous les cas.
1. Caractéristique à vide
Un alternateur triphasé est toujours couplé en « étoile ». C’est pourquoi on présente les grandeurs électriques suivantes :
• Les tensions simples par V .
• Les tensions composées par U .
• Les courants de phase (donc par fil de ligne) par I .
• Le courant inducteur par J.
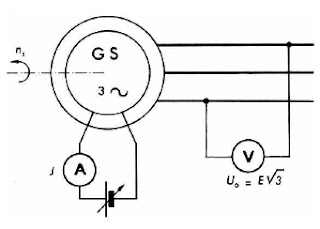
L’alternateur étant entraîné par un moteur auxiliaire à la fréquence de rotation ns et l’enroulement statorique étant ouvert (fig : Schéma de montage), on fait croître le courant inducteur J et on mesure les valeurs correspondantes de la tension entre bornes de phase U0 = E√3 (pour un couplage « étoile »).
On appelle caractéristique à vide d’un alternateur le graphe de la fonction E = f(J).
Comme E est proportionnel au flux utile par pôle Φ, donc proportionnel à B, il s’agit d’une véritable courbe de magnétisation (fig : Courbe de magnétisation).
Caractéristique à vide d’un alternateur
a) Schéma de montage
b) Courbe de magnétisation
La caractéristique à vide comporte deux parties. Lorsque le courant inducteur J est suffisamment faible, E est proportionnel à J : le circuit magnétique n’est pas saturé.
Si le courant J continue d’augmenter, E augmente moins vite : le circuit commence à se saturer.
En général, le point de fonctionnement U0 = Un se trouve dans le « coude » de la courbe de magnétisation, c’est-à-dire le circuit magnétique est déjà saturé.
2.Caractéristiques en charge
2.1. Réaction de l’induit
Comme dans le cas d’une génératrice à courant continu, quand un alternateur débite, le courant de l’enroulement induit crée un champ qui vient perturber le champ de l’inducteur. C’est pour cette raison que ce phénomène est appelé réaction de l’induit.
Cependant, son étude est plus complexe que pour une dynamo. En effet, alors que pour une dynamo l’intensité débité est forcément en phase avec la f.é.m. induite, celle-ci dans le cas d’un alternateur subit un déphasage qui dépend de la nature du récepteur branché à ses bornes : résistance pure, inductance, capacité (fig).
Si la charge est purement résistive (ϕ = 0), comme le champ tournant produit par un stator triphasé est dans l’axe d’une phase quand l’intensité est maximale dans cette phase, on en déduit que l’axe du champ produit par l’induit est perpendiculaire au champ de l’inducteur. Pour cette raison, la réaction de l’induit est dit transversale.
La réaction transversale de l’induit provoque une distorsion du champ dans l’entrefer et une légère diminution du flux utile.
a) Résistance pure
b) Inductance
c) Capacité Alternateur en charge
Si la charge est purement capacitive (ϕ = 90° AV) , quand la f.é.m. induite dans une phase du stator est maximale le courant est en avance de 90° sur cette f.é.m. La réaction de l’induit est aussi longitudinale, mais pour un courant d’excitation donné le flux à travers l’enroulement induit a augmenté, on dit que le champ produit par l’induit est magnétisant.
Donc, si on exprime ce phénomène par une équation électrique adoptant la convention générateur pour chaque phase statorique de résistance R, on aura :
ec = e0 – Lc di/dt , ec – f.é.m. en charge
e0 – f.é.m. à vide
Lc – inductance cyclique du stator
(qui détermine la réaction de l’induit)
Et encore (fig.Circuit électrique), chaque phase du stator se comporte comme un générateur de Thévenin de f.é.m.
E et d’impédance Z = R + jX :
V = E - R I - jX I où : X = ωL – reactance synchrone
Modèle de Behn-Eschenburg d’une génératrice synchrone
Circuit électrique
Diagramme de Fresnel
Cette représentation simplifiée, qui s’appelle le modèle de Behn – Eschenburg, a été faite sous condition que le circuit magnétique n’est pas saturé. Dans ce cas le flux magnétique est proportionnel à l’induction du champ B et respectivement au courant I.
Il permet d’étudier le fonctionnement en charge à partir de la f.é.m. à vide.
2.2. Courbes de fonctionnement
La vitesse d’entraînement d’un alternateur étant constante (vitesse de synchronisme), la tension V (par phase) est fonction de trois paramètres : V = f (I, J,ϕ). Pour simplifier les études on ne fait varier que l’un de ces trois paramètres à la fois.
Dans la pratique, on se limite généralement à la représentation de deux familles de
courbes :
• V = f (I) à J = Cte et cos ϕ = Cte, ce sont les caractéristiques externes.
• J = f (I) à V = Cte et cos ϕ = Cte, ce sont les courbes de réglage.
2.2.1. Caractéristiques externes
Pour relever les caractéristiques l’on dispose des deux méthodes : directe et indirecte. La méthode directe est utilisable seulement pour les alternateurs de faible puissance qui peuvent être mis en état de marche et faits débiter dans différentes charges.
Pour les alternateurs de grande puissance on utilise la méthode indirecte qui utilise les diagrammes vectoriels et les essais à vide et en court-circuit.
Pour représenter la relation f (V, I) pour une valeur de ϕ donnée, on peut utiliser le diagramme simplifié d’un alternateur (fig.2-16a), ce qui donne :
E2 = V2 + (X I)2 + 2 V X I sin ϕ
On en déduit les résultats suivants:
a) Pour cos ϕ = 1, la courbe est une ellipse dont les axes coincident avec les axes de coordonnées.
b) Pour cos ϕ = 0, la courbe est une droite qui coupe l’axe des intensités au point I = E / X.
c) Pour les déphasage du courant en arrière sur la tension, les courbes sont des arcs d’ellipses compris entre les courbes précédentes (fig:a) Caractéristiques externes;b) Courbes de réglage Courbes de fonctionnement) tandis que pour des déphasages en avant, les arcs d’ellipses sont extérieurs. Dans ce deuxième cas, on peut observer un phénomène de surtension (V > E); on peut alors déterminer la valeur maximale de la tension (df / dI = 0, lorsque dV / dt = 0) et la valeur maximale du courant (df / dV = 0, lorsque dI / dV = 0).
a) Caractéristiques externes
b) Courbes de réglage Courbes de fonctionnement
2.2.2. Courbes de réglage
Pour des charges résistives ou inductives, la tension V décroît lorsque I augmente (la réaction d’induit démagnétisante), pour des charges très capacitives (peu fréquentes dans la pratique) la tension V croît avec I (la réaction d’induit magnétisante).
Tout débit sur un circuit inductif oblige le distributeur, pour garder la valeur de la tension V constante, à augmenter le courant d’excitation J de l’alternateur de la centrale. La mise en service d’une batterie de condensateurs, au contraire, l’ oblige à réduire l’excitation (fig : a) Caractéristiques externes;b) Courbes de réglage Courbes de fonctionnement). Ces phénomènes peuvent être employés pour une compensation des effets des charges sur le réseau de distribution.





Aucun commentaire:
Enregistrer un commentaire