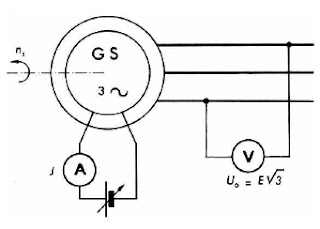
A la différence du transformateur, qui est le plus souvent monophasé, l’alternateur est toujours triphasé.
En effet le fer de l’induit est mieux utilisé car pour un même inducteur, il comporte trois enroulements monophasés indépendants. De plus les machines triphasés à champ tournant (générateurs et récepteurs) ont un fonctionnement plus souple que les machines monophasées à champ alternatif.
Sur la fig:
Alternateur d’expérimentation (Moteurs Leroy). on peut voir les parties d’un alternateur d’expérimentation.
La fréquence f (en Hz) des grandeurs électriques statoriques et la fréquence de rotation n (en tr/s) de l’inducteur sont liées par la relation
f = p n
En Europe et au Maroc on doit avoir f = 50 Hz, si bien que le rotor doit tourner à la
fréquence ns = 50/p (en tr/s), soit en tr/min
ns = 3000 / p
Alternateur d’expérimentation (Moteurs Leroy)
ns est appelé fréquence de synchronisme de l’alternateur.
Le nombre de paire de pôles p dépend donc de la vitesse du moteur d’entraînement; selon cette vitesse on classe les alternateurs en deux grandes catégories.
1. Alternateurs à pôles lisses
Lorsque le moteur est une turbine à vapeur, la fréquence de rotation est nécessairement élevée, supérieure à 1000 tr/min, ce qui laisse deux cas possibles:
• p = 1 ⇒ ns = 3000 tr/min.
• p = 2 ⇒ ns = 1500 tr/min.
Les alternateurs entraînés par une turbine à vapeur ont (en France):
• 2 pôles lorsque Sn ≤ 660 MVA,
• 4 pôles lorsque Sn > 660 MVA.
Rotor. La fréquence de rotation élevée exige que, pour réduire les effets centrifuges à la périphérie du rotor, le diamètre de l’entrefer soit limité; d’autre part, le champ magnétique étant fixe par rapport au rotor, celui-ci n’a pas besoin d’être feuilleté.
En conséquence le rotor se présente comme un cylindre d’acier massif solidaire de l’arbre, dont le diamètre est de l’ordre du mètre; sur la surface cylindrique, des encoches ont été fraisées, parallèlement à l’axe, afin de recevoir l’enroulement inducteur.
L’alternateur est alors dit à pôles lisses ou à entrefer constant (fig: Alternateur à pôles lisses).
Le diamètre étant réduit il faut, pour obtenir des f.é.m. induites notables dans l’enroulement statorique, donner à la longueur axiale de la machine une valeur importante: dans les alternateurs de grande puissance, elle est comprise entre 15 et 20 mètres, ce qui pose des problèmes délicats.
Malgré le diamètre relativement réduit du rotor, les conducteurs de l’inducteur sont soumis à des accélérations radiales considérables (jusqu’à 5000 g). En conséquence, les conducteurs sont maintenus par des clavettes en bronze fermant les encoches; toutes ces clavettes, court-circuitées aux deux extrémités du rotor, constituent une sorte d’enroulement dit “en cage d’écureuil” (indépendant de l’enroulement inducteur) et appelé amortisseurs.
Stator. Le stator est la partie fixe du circuit magnétique; soumis à un champ tournant, il est le siège de courants de Foucault et du phénomène d’hystérésis: par suite il est constitué d’un empilage de tôles d’acier au silicium, perpendiculaires à l’axe de la machine, ayant la forme de couronnes.
Alternateur à pôles lisses
a) Rotor
b) Stator
Sur sa surface cylindrique interne le stator porte des encoches, parallèle à l’axe, régulièrement distribuées, dans lesquelles sont logés les conducteurs de l’enroulement d’induit (fig. 2-4b). Les couronnes du stator, avec leurs encoches, sont découpées à la presse dans les tôles ferromagnétiques.
Lorsque la puissance de l’alternateur est élevée les couronnes statoriques, au lieu d’être découpées d’un seul morceau dans des tôles ordinaires, sont constituées de plusieurs portions identiques en tôles à cristaux orientés: la direction privilégiée de l’acier est disposée suivant le rayon moyen de la portion considérée.
L’alternateur à pôles lisses, entraîné par une turbine à vapeur, équipe les centrales thermiques, classiques (fuel ou charbon) et nucléaire. Il s’agit de machines de très grande puissance: au cours de trente dernières années, leur puissance a augmenté dans des proportions considérables.
La puissance a augmenté beaucoup plus que le volume de la machine grâce à unsystème de refroidissement de plus en plus efficace. L’enroulement statorique estrefroidi par une circulation d’eau très pure (donc isolante); cette eau circule même à l’intérieur des conducteurs de cuivre. Le refroidissement du rotor est généralement assuré par une circulation d’hydrogène sous pression.
2. Alternateurs à pôles saillants
Rotor. Lorsque la turbine est hydraulique, sa fréquence de rotation est toujours très inférieure à 1000 tr/min; or, cette fréquence est la fréquence de synchronisme ns de l’alternateur; celui-ci doit donc présenter un nombre de pôles d’autant plus grand que ns est plus faible devant 3000 tr/min:
ns = 3000 / p ⇒ p = 3000 / ns (ns en tr/min)
Dès que le nombre de pôles est supérieur à quatre le rotor est constitué d’un volant portant à sa périphérie 2p électro-aimants de polarités successives Nord et Sud (d’où le nom de pôles saillants) (fig : Alternateur à pôles saillants).
a) Rotor
b) Amortisseur
Avec cette disposition le nombre de pôles peut être élevé (plusieurs dizaines); mais le diamètre de l’ensemble (appelé roue polaire) augmente avec 2p et peut atteindre 7 à 8 mètres lorsque 2p est de l’ordre de 40 à 60.
Comme pour les alternateurs précédents le rotor étant fixe par rapport au champ, peut être massif; cependant par suite de leur passage devant les encoches du stator, les épanouissements polaires (et parfois même les noyaux polaires) sont feuilletés.
Les alternateurs à pôles saillants possèdent également des amortisseurs (fig. Alternateur à pôles saillants):
ils sont constitués de barres conductrices placées à la périphérie des épanouissements polaires et réunies par des portions d’anneau conducteurs sur les faces latérales (ou même réunies par un anneau complet sur chacune des faces).
Stator. Il est théoriquement identique à celui des alternateurs à pôles lisses mais son
diamètre est très supérieur.
Les alternateurs à pôles saillants équipent les centrales hydrauliques: leur technologie, leur vitesse et leur puissance dépendent de la hauteur et du débit de la chute d’eau (la puissance dépasse rarement 200 MVA).
Le plus souvent l’axe rotorique est vertical; cependant, dans le cas de chute de grande hauteur (plusieurs centaines de mètres) l’axe est horizontal.
Enfin il existe des alternateurs qui constituent, avec leur turbine, des ensembles totalement immergés: on parle de groupes bulbes.
De nombreuses petites chutes (appartenant à des particuliers) sont équipées d’alternateurs à pôles saillants.
Les alternateurs de secours entraînés par des moteurs diesels (hôpitaux, grands magasins...) sont aussi à pôles saillants.
Remarque: Tout alternateur industriel, que son rotor soit à pôles lisses ou à pôles saillants, est nécessairement équipé d’un dispositif spécial appelé système d’excitation dont le rôle est de débiter le courant continu J dans l’enroulement rotorique.
3. F.é.m. à vide
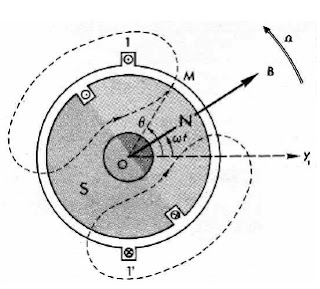
On a déterminé que la f.é.m. induite dans une phase a pour expression :
e = E√2 cos(ωt - π/2) = E√2 sin ωt
avec: E = π√2 N l r n B et ω = pΩ
Il est préférable d’utiliser le flux embrassé par chacune des spires ψ et non l’induction du champ magnétique B.
Chaque phase comportant N/2 spires le flux sinusoïdal ψ a pour expression :
ψ = (2√2 / Nω) E cos ωt = (2√2 / Nω) (π√2 N l r n B) cos ωt
Pour chaque machine donnée (l et r fixés) Φ et B sont proportionnels. Le flux Φ est dû à l’ensemble des lignes de champ issues d’un pôle de l’inducteur et traversant l’entrefer : on l’appelle flux utile par pôle.
Dans le cas d’une machine multipolaire la pulsation ω = pΩ = p(2πn). On doit écrire :
Φ = (2√2 / Nω) E = 2/p l r B
Désormais il est facile d’exprimer la valeur efficace E des f.é.m. induites en fonction de Φ, quel que soit le nombre de pôles :
E = π/√2 N (pn) Φ , mais f = pn
mais f = pn
E = π/√2 N f Φ
Dans tous les raisonnements chaque bobine était supposée repartie dans une seule paire d’encoches ; on parle d’enroulement massé. Cet enroulement massé présente un inconvénient grave – la place disponible le long de l’entrefer est mal utilisée. En réalité les spires de chaque bobine sont disposées dans plusieurs paires d’encoches régulièrement décalées. L’enroulement est dit réparti.
L’enroulement réparti présente aussi un inconvénient : les f.é.m. induites dans les différentes paires d’encoches d’une même bobine ne sont pas exactement en phase.
La f.é.m. induite résultante dans un enroulement réparti est plus faible que dans un enroulement massé.
E reparti = kb E massé
Le coefficient kb est inférieur à 1 et il est appelé
facteur de bobinage.
Dans toutes les hypothèses on suppose que la forme de l’onde de champ magnétique dans l’entrefer est sinusoïdale. La réalité est proche dans les alternateurs à pôles lisses, mais ce n’est pas le cas dans les alternateurs à pôles saillants : l’onde de champ a une répartition qui s’écarte d’une sinusoïde (on atténue le phénomène en augmentant l’entrefer en face des cornes des épanouissements
polaires) (fig. Répartition de l’onde dans l’entrefer d’un alternateur à pôles saillants).
Répartition de l’onde dans l’entrefer d’un alternateur à pôles saillants
Les f.é.m. induites dans les phases ne sont plus exactement sinusoïdales. L’expression de E peut se mettre sous la forme :
E = kf (π/√2 kb N f Φ)
kf est un facteur correctif dit facteur de forme de l’alternateur; sa valeur est légèrement supérieure à 1.
En conclusion, l’expression définitive de E s’écrit :
E = π/√2 kf kb N f Φ
Le produit k = π/√2 kf kb est le facteur de Kapp de la machine : il est toujours voisin de π/√2 = 2,22 (puisque kb < 1 et kf > 1).
4. Enroulement d’induit
0L’enroulement de l’induit d’un alternateur monophasé à deux pôles est beaucoup plus simple que celui d’une dynamo car, le plus souvent, c’est un enroulement ouvert à une seule couche.
L’enroulement, le plus simple, comporte deux brins actifs A et A’ placés dans deux encoches diamétralement opposées (fig.a). Il suffit de réunir ces deux brins sur l’une des faces pour que les f.é.m. engendrées soient à chaque instant montées en série, les deux extrémités libres constituant les bornes de l’alternateur.
On peut augmenter la f.é.m., en multipliant le nombre de brins actifs ; il suffit pour
cela de constituer une bobine (fig.b) dont les parties frontales, appelées têtes,
sont extérieures aux encoches et au champ, donc elles sont inactives.
Enroulement de l’induit
a) Enroulement simple
b) Bobine
c) Schéma panoramique d’une bobine enchevêtrée
d) Schéma panoramique d’une bobine séparée
e) Alternateur à une seule encoche bobinée
f) Répartition parpaire de pôles
g) Gabarit d’une bobine
h) Schéma frontal d’une bobine enchevêtrée
Cette disposition dans deux encoches diamétrales ne suffit généralement pas à répartir la totalité des brins actifs, c’est pourquoi on utilise plusieurs encoches, l’enroulement se présente soit avec des bobines enchevêtrées (fig.c), soit avec des bobines séparées (fig.d). Dans le premier cas, les éléments sont identiques, dans le second l’un est plus étroit que l’autre, mais la f.é.m.; obtenue est la même car
on monte en série les mêmes f.é.m. partielles.
Cependant, quand les brins sont ainsi répartis, ils ne sont plus tous dans des champs de même valeur au même instant et les f.é.m. induites dans les différents éléments ne sont plus en phase ; cela diminue la valeur efficace de la f.é.m. pour la totalité des brins ( facteur de bobinage). C’est d’ailleurs la raison pour laquelle on ne peut bobiner qu’une surface partielle du stator , mais cet inconvénient n’a pas lieu avec les alternateurs triphasés qui sont les seuls utilisés dans la pratique.
Pour les alternateurs monophasés à 2p pôles on va considérer pour simplifier un alternateur à une seule encoche bobinée par pôle (fig.2-7e). Pour mettre en série les f.é.m. induites dans les 2p brins actifs, il suffit d’unir sur l’une des faces, qu’on nomme face arrière, les brins qui se trouvent au même instant dans des champs opposés (1 et 2 par exemple), puis d’unir 2 à 3 sur la face avant.
Enfin, on peut multiplier le nombre de brins par bobine, puis répartir ces bobines dans plus de deux encoches par paire de pôles (fig.2-7f). Dans la pratique, les différentes bobines sont préparées à l’avance sur des gabarits (fig.2-7g) ; elles sont rubanées, imprégnées d’un vernis isolant et étuvées. Il appartient ensuite à l’ouvrier bobineur de les mettre en place dans les encoches, puis d’assurer les liaisons précisées par un schéma frontal (fig.2-7h) ou panoramique.
Dans les alternateurs triphasés on distingue deux catégories :
- Enroulement à une couche
Chacune des trois phases se présente sur le stator comme enroulement d’un alternateur monophasé, celles-ci étant décalées à 120° électriques l’une par rapport à l’autre. Cependant, comme il faut pouvoir les mettre en place sur un même stator, elles occupent un domaine plus faible que pour un enroulement monophasé.
Dans la pratique, on s’arrange pour que toutes les encoches disponibles soient bobinées ce qui fixe l’ouverture d’une phase à 60° électriques.
Dans le cas d’une machine à 2p pôles (soit 2p = 4), on utilise souvent la représentation (fig.2-7h) avec les têtes de bobines repliées sur le flasque afin de permettre la mise en place du rotor.
- Enroulement à deux couches
Alors que l’enroulement à une couche a été l’enroulement de base des alternateurs jusqu’à ces dernières années, on utilise actuellement pour les très grosses unités un enroulement à deux couches (fig:Enroulement à deux couches).
Cet enroulement dont chaque phase a une ouverture de 120° électriques (au lieu de 60° pour l’enroulement à une couche) a une technique de fabrication identique à celle des machines à courant continu.
Il est formé de sections bobinées à l’avance sur gabarits, la section étant formée de deux faisceaux. Comme pour la dynamo l’enroulement d’une machine multipolaire se présente soit comme imbriqué simple (avec retour en arrière après la mise en place d’une section), soit comme un ondulé simple (avec la poursuite en avant pour mettre en série une nouvelle section).
Avec ce type d’enroulement, les têtes de sections forment un ensemble très régulier, ce qui permet de mieux résister aux efforts considérables qui peuvent intervenir en cas de défauts (mise en court-circuit,…). De plus, il est possible de constituer des sections à pas légèrement raccourci afin de réduire certains harmoniques.
5. Plaque signalétique
Elle porte le nom du constructeur et le numéro d’ordre de fabrication, puis des indications techniques (fig:Plaque signalétique d’un alternateur) :
• Nombre de phases
• Puissance apparente utile
• Service
• Tension entre bornes
• Courant débité
• Facteur de puissance
• Vitesse de rotation
• Conditions d’excitation (tension et intensité maximale)
Plaque signalétique d’un alternateur
Sur le contenu de ces données il est bon d’apporter les précisions suivantes :
a) Comme le transformateur, l’alternateur n’a pas comme un moteur, son propre facteur de puissance, celui-ci dépendant de la charge (impédance du réseau) qui est branchée à ses bornes. C’est pourquoi, il ne peut être caractérisé que par sa
puissance apparente puisque, sous une tension constante son débit est limité par l’élévation de température acceptable. Il est souhaitable de faire fonctionner un alternateur, qui alimente un réseau, avec un facteur de puissance égal à l’unité, l’énergie réactive étant produite (ou absorbée) le plus près possible de sa consommation (ou de sa fourniture). Cependant, pour résoudre les problèmes de régulation, cela n’est pas totalement possible, c’est pourquoi, on accepte pour l’alternateur qu’il fonctionne avec un certain facteur de puissance qui est indiqué sur
la plaque signalétique.
b) Un alternateur triphasé est toujours branché en étoile. L’intensité indiquée par la plaque est le
courant nominal par phase In : c’est la valeur efficace du courant le plus intense que peut supporter la machine sans échauffement excessif pour le service indiqué. Ce service peut être continu (c’est-à-dire permanent) ou intermittent. Dans le deuxième cas, il faut prévoir des périodes de fonctionnement à plus faible charge suivant un cycle d’utilisation imposé par le constructeur, sinon la machine risque de
chauffer dangereusement. Si le service n’est pas précisé, c’est qu’il s’agit d’un service permanent à sa charge nominale. La tension indiquée sur la plaque signalétique est la
tension entre fils de ligne, la seule qu’il soit facile de mesurer.
c) Connaissant ces valeurs nominales ainsi que le facteur de puissance pour lequel l’alternateur a été prévu, l’usager pourra facilement déterminer la puissance du moteur d’entraînement. En effet, si on se donne une valeur approximative du rendement η de l’alternateur, rendement d’autant plus élevé que la puissance apparente est plus grande (il est voisin de l’unité pour les turbo-alternateurs), on a :
P = √3 Un In cos ϕ / η
6. Turbo-alternateurs modernes
Généralités. Comme on a déjà signalé le rendement des installations augmente avec la puissance, on a pu assister à une augmentation régulière des puissances des groupes turbo-alternateurs : 200 MW en 1950, 400 MW en 1960, 600 MW en 1970, etc.
Comme les turbines à vapeur s’accommodent bien de vitesses élevées, on les faisait, initialement, tourner à la plus grande vitesse qu’il était possible, c’est-à-dire à la vitesse de synchronisme (soit 3000 tr/mn). Avec cette technique, qui utilise des alternateurs à deux pôles, le diamètre des rotors ne peut pas dépasser une certaine valeur (1,2 m environ) pour assurer une bonne tenue aux frettes qui retiennent les têtes de bobines. Dans ces conditions, pour augmenter la puissance apparente d’un
alternateur , on doit augmenter la longueur du rotor , mais au-delà d’une certaine valeur des phénomènes de résonance mécanique peuvent causer de graves dommages.
C’est pourquoi, pour les très grosses puissances, on utilise des alternateurs à quatre pôles qui sont entraînés à 1500 tr/mn. Les alternateurs les plus récents qui fonctionnent dans les centrales nucléaires françaises ont les valeurs suivantes :
• Puissance nominale apparente : 1650 MVA
• Tension nominale entre bornes : 20 kV
• Intensité nominale : 48 kA
La turbine qui entraîne l’alternateur comporte plusieurs corps (fig) :
• Un premier corps à haute pression
• Trois corps à basse pression

La puissance de la turbine est de 1300 MW (avec un facteur de puissance de 0,9).
L’ensemble turbo-alternateur a une longueur totale de 70 m.
L’alternateur a une longueur totale de 17,37 m et une masse totale de 745 tonnes (fig.).
Le diamètre du rotor, qui est à quatre pôles, est de 1,95 m, sa masse est de 240 tonnes.
La masse totale du groupe turbo-alternateur est de 4900 tonnes (dont 554 tonnes pour les rotors).
Refroidissement des alternateurs par l’hydrogène. Les premiers alternateurs mis en place par l’EDF étaient, refroidis par l’air en circuit ouvert puis, dans une période plus récente, ils étaient refroidis par l’air, qui circulait en circuit fermé.
Actuellement les alternateurs sont refroidis par de l’hydrogène circulant en circuit fermé. Cette solution présente les avantages suivants :
• Les pertes par ventilation sont proportionnelles à la masse volumique du fluide employé pour la réfrigération. Comme la masse volumique de l’hydrogène est 14 fois moins élevée que celle de l’air, les pertes par ventilation seront 14 fois plus faibles .
• La conductibilité thermique de l’hydrogène étant 7 fois plus élevée que celle
de l’air, les échanges de chaleur se font plus facilement avec hydrogène.
Les parties chaudes de l’alternateur cèdent plus rapidement leur chaleur à
l’hydrogène qu’à l’air ; de même, l’hydrogène transmet plus vite sa chaleur
aux tubes du réfrigérant.
• Les échanges de chaleur se font d’autant plus facilement que la pression de l’hydrogène est plus élevée.
L’utilisation de l’hydrogène nécessite d’importantes précautions car l’hydrogène forme avec l’air un mélange explosif quand le mélange contient 5 à 70% d’hydrogène.
L’hydrogène doit être maintenu en pression dans tout son circuit ce qui nécessite une étanchéité parfaite de ce circuit. L’hydrogène situé dans l’enceinte externe de l’alternateur est aspiré par les ventilateurs d’extrémité et refoulé sous les capots (fig.Système de refroidissement à l’hydrogène). Le flux d’hydrogène se divise en plusieurs parties :
• Une première portion assure le refroidissement des têtes de bobine ;
• Une deuxième partie pénètre dans l’entrefer rotor – stator pour sortir par des canaux radiaux pratiqués dans l’empilage magnétique du stator ;
Système de refroidissement à l’hydrogène
• Une troisième partie, intéressant la partie centrale, pénètre par ces canaux radiaux d’une façon centripète (vers l’axe) pour ressortir par d’autres canaux d’une façon centrifuge (vers la périphérie).
• Enfin une dernière partie parcourt les encoches, au sein des conducteurs, dans des tubes prévus à cet effet (fig:Système de refroidissement à l’hydrogène b).
L’hydrogène chaud est dirigé, par un système de cloisonnement, vers les réfrigérants. Ils sont, le plus souvent (au nombre de quatre du type tubulaire) placés à la partie supérieure de l’alternateur.
La réfrigération est assurée par une circulation d’eau provenant des pompes d’extraction du condenseur principal.
Excitation statique. Jusqu’à une époque récente, le courant continu nécessaire à l’excitation du rotor de l’alternateur étant fourni par une génératrice à courant continu montée en bout d’arbre. Le courant continu était transmis au rotor par deux bagues en bronze, le réglage de l’intensité de ce courant étant obtenu par le réglage du courant de l’inducteur de la génératrice. Ce procédé présente les inconvénients suivants :
• La dynamo, en raison de son collecteur, est une machine qui réclame un certain entretien ; de plus, en raison des étincelles du collecteur, on augmente les risques d’explosions .
• Le contact entre les balais fixes et les bagues tournantes est une source d’inconvénients et de pannes.
Les alternateurs modernes utilisent, pour leur excitation, un système statique dit « à diodes tournantes » (fig : Excitation statique « à diodes tournantes »).
Excitation statique « à diodes tournantes »
L’excitation de l’alternateur principal est assuré par un alternateur intermédiaire auquel on adjoint un redresseur à diodes. Cet alternateur a une disposition inversée, le stator étant l’inducteur alors que le rotor est l’induit, ainsi ce dernier (avec son redresseur) peut-il alimenter directement le rotor de l’alternateur principal.
L’alimentation en courant continu du stator de l’alternateur intermédiaire est assurée par un alternateur d’excitation muni d’un redresseur à diodes. Cet alternateur dont la disposition est classique (induit fixe et inducteur tournant) a comme rotor un aimant permanent. C’est au niveau de cet alternateur qu’interviennent les dispositifs de régulation.
C’est ainsi que, pour assurer l’excitation d’un alternateur de 1650 MVA, l’alternateur intermédiaire est une machine à 22 pôles et 39 phases qui, en fonctionnement normal, fournit, par l’intermédiaire d’un pont redresseur à 78 diodes, un courant continu de 6823 A sous tension de 531 V.